シリコン結晶研究のルネサンス
シリコン結晶の内部熱応力による点欠陥の変化
2025/10/21-
初めに
シリコン結晶中には、真正点欠陥によりgrown-in欠陥が発生します。
欠陥は真正点欠陥の他に酸素、炭素、窒素の軽元素中性不純物も含まれることがあります。
発生には、点欠陥や不純物、熱の拡散や、応力が関与しています。
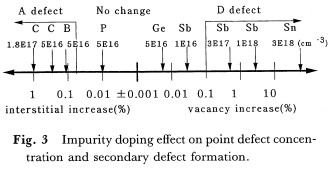
信越半導体の阿部孝夫は、シリコン原子と大きさの異なる元素の高濃度ドープによる応力と、成長結晶中の温度分布による内部熱応力が、優勢真性点欠陥の種類と濃度を変えて、grown-in欠陥の種類と密度を変えることを立証又は予言しました。
我々はそれを現象論的定量的に解析しました。
熱応力については、2014年に大直径結晶で熱応力による空洞欠陥の増加が実験とシミュレイションにより報告され立証されました。
大直径結晶の高品質化と結びつきました。
不純物の場合は別ページに述べます。
大直径結晶中心部の内部熱応力による空洞欠陥の増加
初めに
1. 背景
1982年、阿部の予想
Microdefects and Impurities in Dislocation-Free Silicon Crystals
Takao Abe, Hirofumi Harada & Jun-Ichi Chikawa
MRS Online Proceedings Library 14, 1-17 (1982). https://doi.org/10.1557/PROC-14-1
https://doi.org/10.1557/PROC-14-1
Abstract
It was observed that swirl defects are formed when the temperature gradient near the interface is high, and that their formation is suppressed by doping nitrogen.
コメント
「温度勾配が主、成長速度は従」という主張の始まり
1983
Swirl defects in float-zoned silicon crystals
T.Abe?H.Harada?J.Chikawa??
Physica B+C, Volume 116, Issues 1-3, February 1983, Pages 139-147
https://doi.org/10.1016/0378-4363(83)90241-3
temperature gradient at the interface associated with the growth rate is the critical condition for formation of both the defects rather than the cooling rate.
(1) It produces a high stress field to expand their sizes.
(2) It decreases concentration of vacancies by out-diffusion to lower the effect by mutual annihilation of interstitials and vacancies.
the temperature gradient at the interface play an important role for swirl formation.
The growth rate required for suppression of swirl formation decreases with increasing the diameter
コメント
「温度勾配が応力を作る」という基本主張の始まり
1990
シ リ コ ン結 晶 中 の 点 欠 陥 と二 次 欠 陥
阿 部 孝 夫
応用物理, 59(3), 272 (1990).
大 直径化 とともに半径方向の温度こう配が増大するので,酸 素誘起の積層欠陥(OSF)の 制御が因難になる
温 度 こ う配 説 を 提 案 し て き た23,24).
23) T. Abe, H. Harada and J. Chikawa: Physica, 116B (1983) 139.
24) T. Abe, H. Harada and J. Chikawa: Defects in Semiconductors, ed. J. W. Corbett and S. Mahajan, Mater. Res. Soc. Symp. Proc. Vol. 14 (Elsevier, New York, 1983) p. 1.
2.4成 長中温度こ う配 と点欠陥
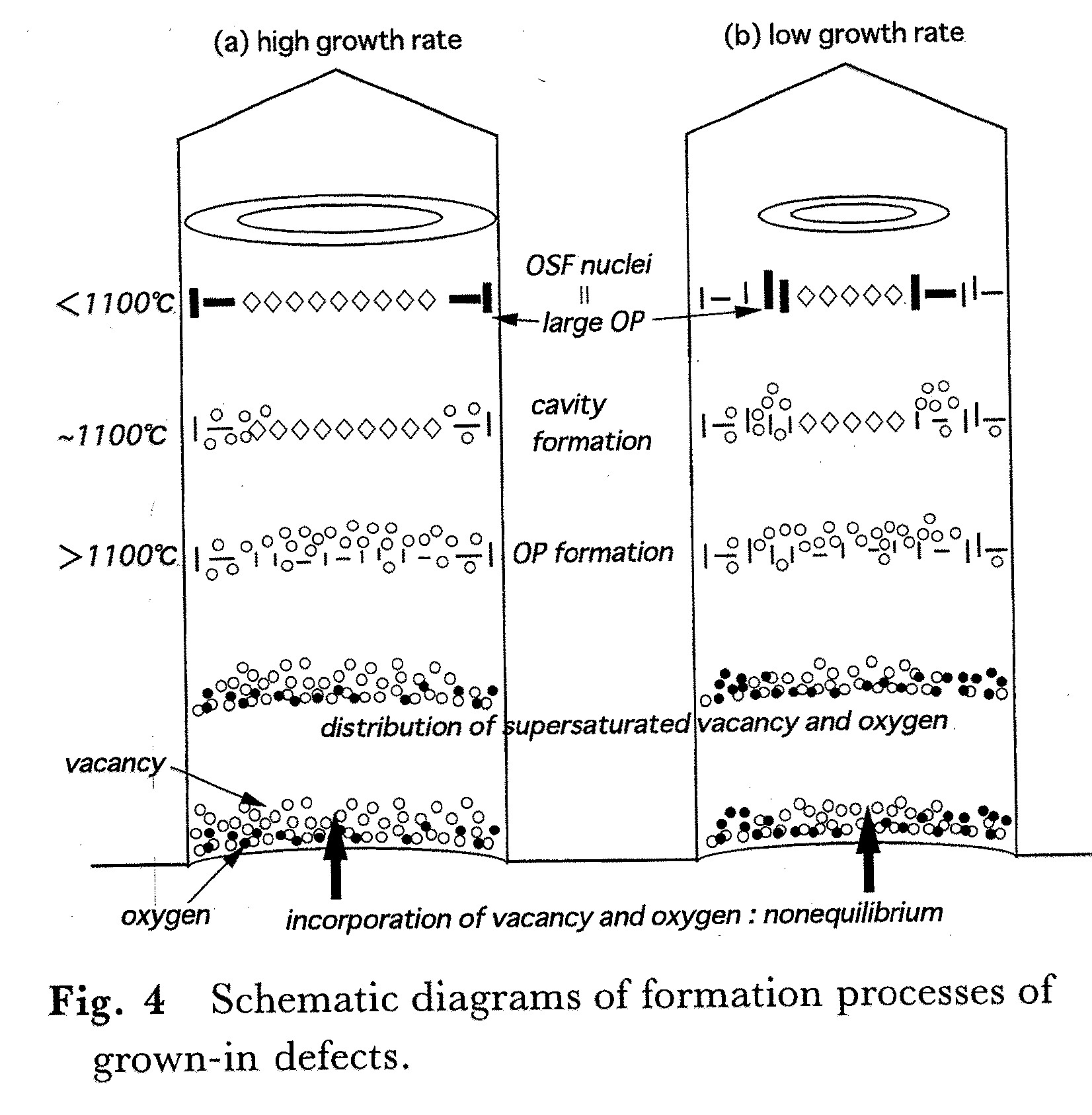
直径 を一定 にして成長速度を低速にするとA欠陥が発生 し,高 速にするとD欠 陥が発生す る.一 方,低 速 では結晶の成長方 向に温度 こう配 が大 に なり,高 速で は温度 こう配 が小 にな ることがわか ってい る.
ま た,成 長速度を一定 に して直径 が小 さいときA欠 陥が発生 し,直 径 が大 きいときD欠 陥が発生す る.容 易にわか るように温度 こう配 は 直径小 のとき大で,反 対 に直径大 の と き小 で
(2)成 長 が 停 止 す る と, 2.4節 か らわかる よ うに温 度 こ う配 が 大 にな り,成 長 界 面近 傍 では空 孔(V)に 代 わ って 格 子 間 シ リコ ン(I)濃 度 が高 ま る.
5.完全結晶の成長条件とシミュレーション
A欠陥やR-OSFが結晶の外周部に発生し, D欠陥やAOPが中心部にできる理由を,塚田ら48)のCZ結晶の成長中の熱応力解析の計算結果を用いて説明する.図17は成長界面が融液に対して,凹の場合の成長方向の温度分布(a)と最大せん断応力分布(b)である.注目すべきことは,図17(b)に示すように(1)応力は成長界面近傍に集中している. (2)特異点Pがあり,それより中心部は圧縮応力,外周部は引っ張り応力になっていることである.例えば,図7ではP点は内側のN領域に相当する.もちろん,この応力分布は各要素に分解して検討すべきであるが,ここでは圧縮応力が空孔,引っ張り応力が格子間シリコンを発生させるという定性的な説明にとどめる.
コメント
特異点Pがあり,それより中心部は圧縮応力,外周部は引っ張り応力になっている
圧縮応力が空孔,引っ張り応力が格子間シリコンを発生させるという定性的な説明
が主張の基礎になっている
1992
Dynamic Behavior of Intrinsic Point Defects in FZ and CZ Silicon Crystals
T. Abe and H. Takeno,
MRS Proceedings, Volume 262, 3 (Materials Research Society, 1992). Journal: MRS Online Proceedings Library Archive /
https://link.springer.com/article/10.1557/PROC-262-3
Almost all crystals have defect boundaries between periphery and center region which may be attributed to a stress field in the crystals during growth.
コメント
1990年応用物理の英語版
2000
The formation mechanism of grown-in defects in CZ silicon crystals based on thermal gradients measured by thermocouples near growth interfaces
T. Abe
Materials Science and Engineering: B, Volume 73, Issues 1-3, 3 April 2000, Pages 16-29
https://doi.org/10.1016/S0921-5107(99)00428-6
Abstract
We propose that large G produces shrunk lattice spacing and in order to relax such lattice excess interstitials are necessary.
コメント
温度勾配は、巨視的なもので、Voronkovの界面直近だけとは異なる、ごっちゃにしているので的外れ
「温度勾配が大きいと格子が縮み、interstirialが発生する」は誤り
OSF領域は空孔が多く酸素析出が促進され、後の熱処理で酸素析出によりinterstitialが発生し積層欠陥になるのを、成長中にinterstirial-richになると勘違いl
2011
Intrinsic point defect behavior in silicon crystals during growth from the melt: A model derived from experimental results
TakaoAbeToruTakahashi
Doi: 10.1016/j.jcrysgro.2011.07.027
By increasing the thermal gradient, which can be controlled by lowering the growth rate, the vacancy (AOP) region is reduced, due to the generation of a silicon interstitial-rich region.
コメント
「温度勾配はinterstitialを増やす」と単純化しているが誤り
まとめ
温度勾配と内部熱応力により真正点欠陥の種類が変わることを主張した。
「Voronkovの温度勾配/成長速度説」をこれにより批判したが、温度勾配が巨視的と微視的の別物であり、見当はずれ
「大直径結晶の中心では圧縮応力によりvacancy-richになる、外周ではその反対」が正しい
大直径では応力が重要で、Voronkov説は修正必要
それ以外はVoronkov説が有効
2. 成長中の内部圧縮熱応力による空孔型欠陥の増大の現象論的解析
初めに
我々は1999年に、阿部の予言の現象論的定量的解析を行った。定性的には、定量的にはドーパントの場合と比べて小さかった。
しかしほぼ同時期に、新しいヤング率の測定と応力のシミュレイションが行われ、用いたデータより数桁大きいことが報告された。
それを用いるとドーパントの場合と同等の点欠陥の増加の大きさが得られた。
その後15年ほどたって、次項に示す実験的確認が行われた。
今ではシリコン結晶製造に無くてはならない指針となっている。
内部応力の効果は「格子不整合薄膜中の拡散が、応力による過飽和真正点欠陥に影響される」で定量的に解析された先行研究がある。
2.1. 予備的考察
「CZシリコン結晶における点欠陥の挙動」
棚橋克人,井上直久,溝川悠介,
第37回真空に関する連合講演会(10月30~11月1日,大阪).(1996)
Behavior of Point Defects in CZ Silicon Crystal Growth
K. Tanahashi, N. Inoue and Y. Mizokawa
1996 Materials Research Society Fall Meeting, (Nov. -Dec. , Boston, USA)
The effect of internal stress on the behavior of point defects in growing silicon crystals
K. Tanahashi, M. Kikuchi and N. Inoue
Gordon research Conference on Point & Line Defects, Colby Sawyer,, July 12-17(1996)
シリコン結晶中の成長時導入欠陥の巨視的分布の発生*
棚橋克人*1・井上直久*2・溝川悠介*1
真空、1998 年 41 巻 3 号 p. 104-107
https://doi.org/10.3131/jvsj.41.104
今回我々は,固液界面の温度変動や成長速度に伴い酸素や空孔が結晶中に非平衡に取り込まれると考えた.空孔の取り込みに関してはWebb16)や Bolling17)の報告がある.彼らは成長速度の増加に伴い空孔の取り
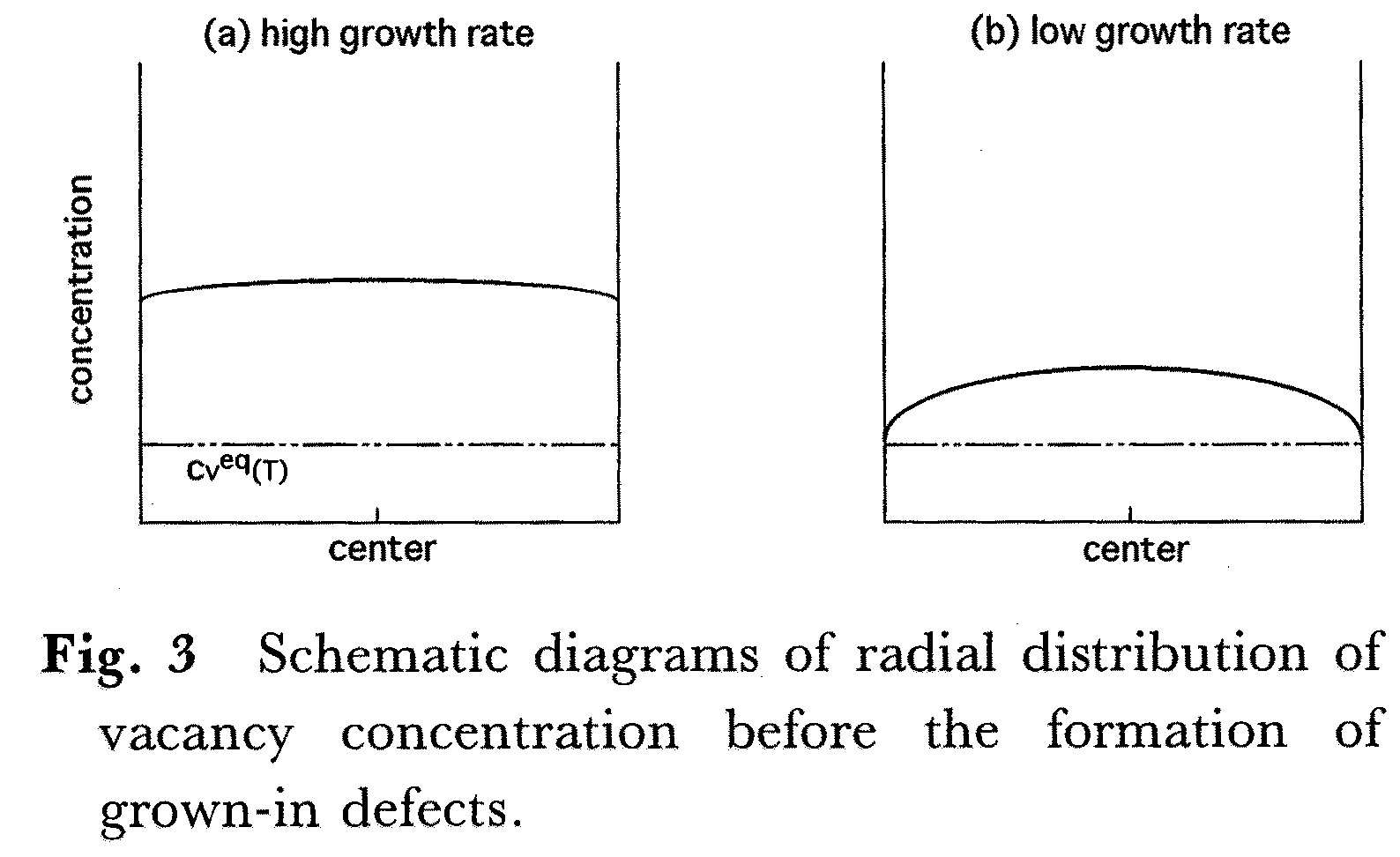
込み量が増加することを報告している.さらに径方向分布については応力の影響を考慮する必要がある18).中心部は温度勾配によって圧縮応力が発生するため,外周部より空孔濃度が高くなる18).
18) シ リ コ ン結 晶 中 の 点 欠 陥 と二 次 欠 陥、阿 部 孝 夫、応用物理, 59(3), 272 (1990).
内部応力の効果を、ドーパントでは熱力学の基礎を、熱応力では薄膜の拡散の研究を踏まえて解析。
Nonequilibrium thermodynamic analysis on the behavior of point defects in growing silicon crystals: effects of stress
K. Tanahashi and N. Inoue
Materials in Electronics, 359-363 (1999)
Point defect concentration in a growing silicon crystal
K. Tanahashi,T.Higashino, M. Kikuchi and N. Inoue
Gordon Research Conference on Materials Processes Far From Equilibrium
2.2. 既存データを用いた解析
内部熱圧縮応力によって、空孔の形成エンタルピが下がり、平衡濃度が増すという考え
以下は熱力学の教科書で見られる。ここでは鹿児島大学中村祐三先生のHPから転載させていただいた。
http://www.mech.kagoshima-u.ac.jp/~nakamura/bussei/thermo-point-defect03.pdf
1.空孔の平衡濃度
空孔の形成エネルギ
N 個の原子が占める格子点があり、そのうち n 個が空位、すなわち空孔が置き替わるものとする。こ
のとき、着目する格子点にある原子を結晶から取り去ってしまうと、原子の総数が n 個だけ減ってしま
う。原子の総数は変わってはいけないので、一旦取り去ったこれらの原子は結晶の表面に置くことにな
る。よって、空孔の形成は体積の膨張を伴う。このようにして、結晶内から1個の原子を取り出し表面
に置く仕事が、1個の空孔を形成するために必要なエネルギーであって、これを EFVとする。
EFVをどのように評価するかを、上のプロセスに従って考えてみよう。
まず、結晶中にある1原子が、そのまわりにZ個の原子で囲まれているものとする。原
子間結合がこれらのZ個の最近接の配位原子のみによって与えられると仮定すると、原子を取り去るエネルギーは
Eremove = Zεbで与えられる。ここで、εbは個々の原子間の結合手の結合エネルギーである。
次に、取り去った原子を表面に置くと、表面の原子と結合することになる。結晶内から取り除かれた
多数の原子が表面に置かれた場合、それらが結合してあらたな表面を形成するとすれば、
それらの原子の結合手は表面の法線方向だけが繋がっていないので、
Esurface = (2/3)Zεb
だけエネルギー的に安定となる。これより、空孔を作るエネルギーはおおよそ
EF V = Eremove - Esurface = Zεb/ 3
となる。
ここで固相から直接、気相に変化する昇華(sublimation)のエネルギーを Esubと
すると、これは結晶を構成する原子間の結合手がすべて切るために必要なエネルギーであ
るから、
Esub
= zεb
である。よって、
(2)空孔の熱平衡濃度
元々N個の原子で占められていた格子点のうち、n個を空孔に置き換えると、結晶の
エンタルピーの変化は
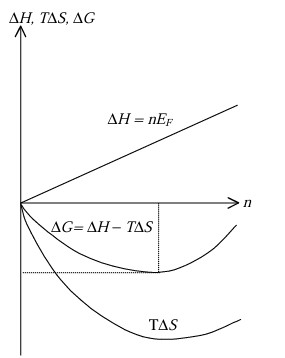
Δ H=nEF
で与えられる。
次に、n個の空孔をN個の格子点に配置する場合の数は、
W = N)!/ (N-n)!n!
である。ボルツマンの関係より、空孔の混合によるエントロピーの変化は
ΔS = kBlnW=kB [lnN! - ln(N-n)! - lnn!]
で与えられる。また、空孔を形成した際には、その周りの原子の振動が変化するために、エントロ
ピーが変化する。そこで、1個の空孔形成に伴う振動エントロピーの変化をΔSvibとする。よって、
ギブスの自由エネルギーの変化は
ΔG = ΔH -TΔSmix - TnΔSvib
= nEF- kBT[lnN! - ln(N - n)! - lnn!] - TnΔSvib
である。右の図に示すように、エンタルピー項ΔHは空孔の数に比例して増加するが、エントロピー
項(-TΔSmix-TnΔSvib)は最小値をもつため、自由エネルギーΔGも最小値をもつ。
ここで、N ,n >> nNのときには、以下のスターリングの近似式
lnN! = NlnN-N
ln(N - n)! = (N - n)ln(N-n) -(N-n)
ln n!= nlnn-n
が成り立つことから、自由エネルギーの変化は
ΔG = nEF - kB T[NlnN - (N-n)ln(N-n) - nlnn] - TnΔSvib
と近似できる。ここで、系が平衡状態となるには、ΔGが最小でなければならない。すな
わち、
0= ∂ΔG/ ∂ n = 0
であることが条件となる。先に求めた近似式を用いて、これを計算すると、
∂ΔG/ ∂ n = = EF - kBTln (n/(N-n)) -TΔSvib = 0
となる。空孔濃度を、原子の占めうる全格子点に対する空孔の割合として
CV = n/N
で定義すると、n N>>のときには、
CV = n/ N = n/(N-n) = exp (ΔSvib/ kB) exp(- EF/ kBT)
で与えられる。 exp(ΔSvib /kB)は温度に依存しない。よって、Aを定数として
CV =AVexp(- EF/kBT)
を得る。金属においては、 A=1~10である。
(3)空孔濃度に対する応力の影響
結晶に
等方的な引張の応力σが作用している状態を考える。空孔を形成する際には、
こ
の応力によって力学的な仕事がなされ、空孔の形成を助ける。今、空孔の体積をΩとする
と、その仕事は
W = σΩ
となる。よって、一個の空孔を形成するための正味のエネルギーは、
EF* = EF - W = EF -σΩ
で与えられ、空孔濃度は、
CV (σ) = Aexp( -EF*/ kBT) = Aexp{-(EF-σΩ)/ kBT} =CV exp(σΩ/kBT)
となる。従って、等方的な引張応力σがある場合とない場合の空孔濃度の差?CVは、
ΔCV = CV(σ) - CV = CV{exp(σΩ/kBT}-1}
で与えられることになる。応力が小さく、Ω<<kBTのときには、
exp(σΩ/kBT) = 1+σΩ/kBT
であることから、
ΔCV = (σΩ/kBT)CV
となる。応力の影響を加味したこれらの式は、高温で応力を付加された材料の変形が原子
の拡散によって生じるクリープ挙動を評価する際に重要となる基礎式である。
関連研究
初めに
我々は内部応力の効果について、大きさの違うドーパントと熱応力というバルク結晶の2つの場合を一緒に、平衡濃度の増大効果として検討しました。
その際参照したのが、格子定数の異なる結晶のヘテロエピで、内部応力による点欠陥の濃度の変化で、拡散を説明した物でした。
しかし、それらの研究の源流は圧力下や応力下のドーパント拡散でした。
以上の現象はこれまで互いに独立に検討されてきましたが、ここではそれらを源流から横断的に取り上げていきたいと思います。
Si中のP拡散のペア拡散モデル
P拡散では色々な異常が観測されていました。それに対して電電公社の吉田正幸らは「V-P pair diffusion model」を提案しました。これは現在ではドーパント拡散のシミュレイションの基盤となっています。
M. Yoshida:Jpn . J. Appl. Phys. 10 (1971)702.
M. Yoshida, E. Arai, H. Nakamura and Y.Terunuma: J. App1. Phys, 45 (1974) 1498,
M. Yoshida:J. Appl. Phps. 48 (1977) 2169.8
M. Yoshida;Jpn. J. Appl. Phys. 18 (1979)479.
M. Yoshida:Jpn . J. Appl. Phys. 19 (1980)2429.
など
シリコン結晶の不純物拡散機構
吉 田 正 幸
応用物理 第50巻 第1号 1, ((1981)
It is natural to assume that group V impurities diffuse in silicon -by a vacancy mechanism,
because they occupy substitutional sites. Based on the pair diffusion model that the
impurities diffuse in silicon only via the diffusion of impurity-vacancy pair (E center),
anomalous diffusions of phosphorus and arsenic can be explained.
On the other hand the relation between the enhancement of diffusion and the growth
of extrinsic stacking fault during oxidation can be explained only on an interstitialcy
mechanism.
Therefore it is the purpose of present note to introduce the recent studies of a vacancy
and an interstitial silicon and to discuss the diffusion mechanisms of impurities. Even if the
interstitialcy mechanism is correct, the impurities should diffuse likewise only via the diffusion
of the pair of an interstitial silicon and an impurity. Therefore the atomistic model of this
pair should be studied for the interstitialcy mechanism.
シリコン結晶中のリン拡散におけるリンー空孔対拡散モデル
吉田正幸
応用物理 第64巻 第11号(1995)
シリコン結晶中のリンと空孔との間には大きな結合エネルギ-があるので,リンが空孔機構で拡散する場合,リンと空孔が対となって拡散する(対拡散モデル).この対が解離すると過剰空孔が発生する.結合エネルギーが大きいので,リンと空孔とが離れていても,それらの間には大きな相互作用がある.そのためリン濃度の増加につれて擬空孔形成エネルギーおよび結合エネルギーが減少する.これらによりシリコン結晶中のリンの異常拡散は説明できる.対拡散モデルは集積回路製作における不純物拡散工程のシミュレーションに重要な役割をはたしている.
Eセンター(V-P)のvolume of formationは実験的に10Å3とされている
Barnes, C. E. and Samara, G., in Microscopic Identification of Electronic Defects in Semiconductors,
edited by Johnson, N. M., Bishop, S. G., Watkins, G. D.,
Materials Research Society Symposia Proceedings, Vol. 46 (Materials Research Society, Pittsburgh, PA 1985), p. 471.
拡散に対する静水圧(外部応力)の効果
緩和体積が議論されている
Pressure and stress effects on diffusion
A.Antonelli and J. Bernholc,
Phys. Rev. B 40, 10643 (1989)
DOI: https://doi.org/10.1103/PhysRevB.40.10643
Pressure and stress effects on diffusion
A.Antonelli and J. Bernholc,
Mater. Res. Soc. Symp. Proc. 163, 523 (1990)
中性空孔の隣の原子は内方向へボンド長の3%relaxし、周りの体積が4.9Å3減少する。vacancyのrelaxation volume Ωr -5Å3
原子体積は20Å3(5x1022/㎝3),formation volume は15Å3.
Vacancy in Silicon Revisited: Structure and Pressure Effects
Alex Antonelli, Efthimios Kaxiras, Jim Chadi
1998Physical Review Letters 81(10):2088-2091
DOI: 10.1103/PhysRevLett.81.2088
Si中の拡散に対する内部応力の効果
吉田らのグループは、Si表面の窒化膜被膜の応力の拡散への影響を調べた。
表面近くの応力により点欠陥の濃度が変化すると考えた。
Effect of Stress in the Deposited Silicon Nitride Films on Boron Diffusion of Silicon
K. Osada, Y. Zaitsu, S. Matsumoto, M. Yoshida, E. Arai and T. Abe
Journal of The Electrochemical Society, Volume 142, Number 1, 202
Citation K. Osada et al 1995 J. Electrochem. Soc. 142 202
DOI 10.1149/1.2043867
格子不整合薄膜の拡散への応力効果
初めに
下記論文のabstractにおいて、格子不整合のヘテロエピでは、膜間に応力が働いており、外部圧力とは異なる状況で、空孔や格子間原子は内部応力による緩和体積分の自由エネルギ変化のため、平衡濃度が異なっていることを論じている。以上の考え方は、拡散への効果であるかどうかに依らない。
1993
N. Moriya, L. C. Feldman, H. S. Luftman, C.A. King, J. Bevk, and B. Freser, Phys. Rev. Lett. 71, 883 (1993).
Boron diffusion in strained Si1-xGex epitaxial layers
Phys. Rev. Lett. 71, 883 - Published 9 August, 1993
DOI: https://doi.org/10.1103/PhysRevLett.71.883
守矢は歪SiGe中でBの拡散が遅くなることを報告した。その理由を歪によりbandgapが狭まり、charged点欠陥の濃度が変化するためと説明した。
1996
Interdiffusion mechanisms in coherently strained SiGe multilayers
N.E.B. Cowern, W.J. Kersten, R.C.M. Dekruif, J.G.M. van Berkum, W.B. de Boer, D.J. Gravesteijn, C.W.T. ulle-Liewma,
in: G.R. Srinivasan, C.S. Murthy, S.T. Dunham (Eds.), Proceedings of the 4th International Symposium on Process Physics and Modeling in Semiconductor Devices,
Electrochem. Soc. Proc., Vol. 96-4, Electrochem. Soc. Pennington, NJ, 1996, p. 95.
歪SiGe中のドーパント拡散は、組成や歪や点欠陥の熱平衡からの過飽和度に影響されると考えられる「。
守矢はSiGe中でBの拡散が遅くなることを報告した(1993年)。
格子間原子の周りでは緩和し空孔の周りでは収縮する。外圧のない場合は形成体積Ωfは無視でき緩和体積Ωrが寄与する。格子間と空孔では符号が反対である(緩和体積は格子間では+、空孔は-)。
formation volume Ωf
関連文献
1998
Pressure and Stress Effects on Defects and Dopant Diffusion in Si
Michael J. Aziz
Special issue on "Ten Years of Diffusion in Silicon", Defect and Diffusion Forum 153-155, 1-10 (1998).
Si/GexSi1-x
page. 5
Ce(σ)/Ce(0) = exp (σVf/kBT) , (7)
拡張 内部熱圧縮応力による空孔平衡濃度の増加
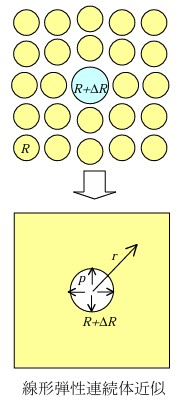
上記のように通常は応力とは外部からの圧力が考えられており、空孔の形成は不利で平衡濃度は減少する。しかし以下に述べるように、
等方的な内部圧縮応力σが作用している場合には、空孔形成により表面への原子体積の増加と、内部への緩和体積の減少Ωrelが起きる。(上の図でΔRがマイナス)
表面では圧力がないため仕事はせず、内部では圧縮下で体積が減るためにエネルギが減るので有利となり、平衡濃度が増えると考えられる。
ΔCV = (σΩrel/kBT)CV
(上下記Cowern, Aziz論文参照)
CZ -Si晶成長における点欠陥の挙動-応力・不純物の効果, 表面と界面, 温度勾配の効果
井上直久,棚橋克人, 森 篤史*
日本結晶成長学会誌、26-5, 243-249 (1999).
§3 点欠陥濃度に対する応力の影響め
3.1 熱応力の効果
我々はその代りに、成長中の温度勾配による内部応力が点欠陥の濃度に影響している可能性について考察した。点欠陥に対する応力の効果は平衡濃度に対するものと拡散係数に対するものとが考えられる。
平衡濃度の変化は形成の自由エネルギーに対する効果から生ずる。通常---(
緩和体積 VF = -αΩ)Ω は原子体積α緩和体積の割合、0.3程度
通常の 考 え方 で は§2 で 述 べ た よ うに , 格 子 間 原 子 を作 る に は 表面の adatom を取 り込 む た め 体積が減 少 し ((緩和体積 VF = -αΩ)Ω は原子体積,α緩和体積の割合、0.3程度
,空 孔で は 表 面 に 放 出す る た め 体 積 が 増大 する (VF= Ω >0).詳 し く考え る と格 子 間 原子が できる と周 りの 原 子 を 押 し広 げ (緩 和 体 積 VF' =α Ω> 0),空孔 で は 反 対 とな る が ,原子 1 個 の 変化ほど で は な い (α < 1)た め 差 し 引 ぎ (VF =(1一α)Ω> 0)で は 前者 の 効果の 方 が 大 きい .
した が っ て 良く知 られ て い る よ うに 外 部 圧 力下 で は 格子 間原 子形 成 の 仕 事 は 一,空孔 形 成 の 仕事は + と な り,格子間 原 子 の 平 衡濃度は 増大 し空孔 の 濃度 は 減少する .
しかし、内部応力の効果は反対と考えられている。その理由は 表面で の 体積変化 は 表 面 で の 応力が 0 の た め 仕 事 を伴 わ な い の で ,緩 和 体積 だ けが仕事 に 関係す る た め で あ る .
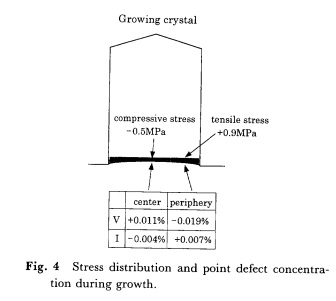
まず定 性的 に
は Fig.4 上 半 に 示 す よ うに 結 晶 の 中 心 は 圧 縮応力,外周は 引 っ 張 り応 力 で あ るか ら,中心 で は 空
孔が 増 大 し格子 間 原子 が 減 少 し ,外周 で は 格子 間原 子 が 増大 し空 孔が減少 し て い る と考え ら れ る .
定 量的 に は , 結晶成長 中の 温 度 勾配 に よ る応力 はσz= 一αE / (1 ? ν){d2T/dz2一 T} (14)
で 与 え られ るが , こ れ を 用 い て 弾性 率 の 温 度 依 存性 を 考 え応 力を 計算す る と界面 付近 で は 中心 で 約
O.5・MPa ,外周 で 約 0.9MPa とな る . した が っ てσ VF = 0.01 meV とな っ て , 点 欠 陥 の ,応 力 の 無
い と きの 平 衡濃 度 か ら の 変化量 は ほ ぼ
ΔCeq/Coeq= 0.01% (15)
と な る .図 の 表 に は それ ぞれ の 変 化を 示 し た .今後結晶径 が 増 す と同 じ引 ぎ上 げ 速度 で は 応力は 大
き くな り, 濃 度 変化 も大 ぎ くな る と考 え られ る .
 原子半径の異なる不純物ドープの場合に、0.1-1%でgrown-in欠陥が増えていると見られるのに比べて1桁小さい。
原子半径の異なる不純物ドープの場合に、0.1-1%でgrown-in欠陥が増えていると見られるのに比べて1桁小さい。
参考文献(2001年下記文献に引用)
K. Tanahashia,b,*, N. Inouea, Y. Mizokawab,
Physica B 308-310 (2001) 502-505.
[8] N.E.B. Cowern, W.J. Kersten, R.C.M. Dekruif, J.G.M. van Berkum, W.B. de Boer, D.J. Gravesteijn, C.W.T. ulle-Liewma,
in: G.R. Srinivasan, C.S. Murthy, S.T. Dunham (Eds.), Proceedings of the 4th International Symposium on Process Physics and Modeling in Semiconductor Devices,
Electrochem. Soc. Proc., Vol. 96-4, Electrochem. Soc. Pennington, NJ, 1996, p. 95.
3.1. Anisotropy of the work under the anisotropic stress field around impurity
Here, we consider that the relaxation volume under the anisotropic stress field ΔVF is changed anisotropically from that under the isotropic stress to relax anisotropic stress.
4. Analysis of void density change by the stress due to impurity doping
Only unknown parameter for calculation is ΔVR: It is assumed to be 6.67 A3 (1/3 of atomic volume of silicon).
Concentration of point defects changed by thermal stress in growing CZ silicon crystal: effect of the growth rate
K. Tanahashi,*, M. Kikuchi, T. Higashino, N. Inoue, Y. Mizokawa"
Journal of Crystal Growth 210 (2000) 45}48
2.3. 新データと先行研究を用いた再計算
上の発表から少し遅れて、ヤング率の測定と、大直径結晶の応力のシミュレイションが行われました。ヤング率は温度依存性が既報では1eVと推定されたのに対して0.0027eVと小さいため融点での推定値が従来のとなりました。応力は以前のせん断応力の0.5MPaから直径cmでの推定圧縮応力のとなりました。
これを用いると平衡濃度は従来データを用いた増加0.01%から
ΔCV = (σΩrel/kBT)CV
ヤング率測定
N. Ono, K. Kitamura, K. Nakajima, and Y. Shimanuki
Jpn. J. Appl. Phys. 39, 368 (2000).
Global simulation of the CZ silicon crystal growth upto 400mm in diameter
K. Takano*, Y. Shiraishi, J. Matsubara, T. Iida, N. Takase, N. Machida, M. Kuramoto, H. Yamagishi
Journal of Crystal Growth 229 (2001) 26-30
The mechanical properties of silicon are 1.56E+5MPa for Young's modulus, 0.26 for Poisson ratio, and 3.72E-6K 1 for the thermal expansion coefficient.
直径30㎝の中心で20MPa
空孔の緩和体積
Vacancy in Silicon Revisited: Structure and Pressure Effects
A. Antonelli, Efthimios Kaxiras, D. J. Chadi
Phys. Rev. Lett. 81, 2088 - Published 7 September, 1998Erratum Phys. Rev. Lett. 83, 1077 (1999)
Ce/C0e =exp (σΔVF/kT )
kBT =2.337x10-20 m2 kg s-2
σz = 10MPa
ΔVr = -5 Å3, ΔVF = 15 (20-5) Å3
σzΔVF = 4.34x10-22 kgm2s-2
σzΔVF/kT = 1.857x10-2
exp (σΔVF/kT )= 1.0187
空孔の平衡濃度が2%増加
これは、大きさの異なる不純物の高濃度ドープによる欠陥の増加の目安0.1-1%に匹敵し、大直径結晶の空洞型欠陥の増加を支持する。
実験での確認
2014年に、大直径結晶でVoronkov criterionからの外れが報告されました。
また、Voronkovの式を拡張し、温度勾配と応力のシミュレイション値を代入して、
残された課題
初めに
「大直径結晶の中心部ではでは内部熱圧縮応力により界面での空孔の平衡濃度が増加し空孔型の空洞欠陥が発生する」
という「阿部の予想」、「井上らの現象論的解析」が実験的に確かめられ、「grown-in欠陥フリーの大型結晶の成長」が確立されつつあります。
しかし、以下の事が残っています。
界面での平衡濃度の増大から、空洞の発生までの道筋。
平衡濃度の増加量
応力と温度勾配の実際の値
その他に「温度勾配と成長速度の関係」があります。温度勾配と応力のシミュレイションの妥当性に関わります。
平衡濃度の増加量と二次欠陥の発生
初めに
内部応力により、grown-in欠陥が空孔又は格子間型になることについて、応力による融点での平衡濃度の増大が0.1-1%に増えると見られます。
どのような機構に依るのかを考えます。
欠陥の発生する温度で、点欠陥の過飽和度が閾値を超えると考えることができます。
融点・界面から冷却中に、点欠陥の対消滅により濃度が下がる一方で
高濃度領域から低濃度領域への拡散が進みます。
冷却により平衡濃度が下がります。
応力のない場合でも同様ですが、応力がある場合により高い温度で、過飽和が始まると見られます。
冷却と界面から遠ざかることによって、平衡濃度の増加は減少します。
温度勾配と成長速度の関係
Voronkovの式の拡張、圧力と内部応力の違いが分からず
2011年にVanhellemontらはVoronkovの式に応力の項を追加しました。
しかし、内部応力と外部圧力の区別ができないため、圧縮応力下で空孔が減少するという実際とは反対の結果になってしまいました。
我々の結果を、間違いと主張しましたが、誤りでした。
但し、Yang率はOnoの、応力はTakanoの、上に引用した、大きな値を用いたため点欠陥変化の絶対量は0.5%程度と見積もり、我々の見積もりも同じ程度になると指摘し、応力効果が起こりうると考えました。
Intrinsic point defect incorporation in silicon single crystals grown from a melt, revisited
Jan Vanhellemont
J. Appl. Phys. 110, 063519 (2011)
DOI: 10.1063/1.3641635
末岡の解析
末岡は2011年にVanhellemontの式を用いながら、我々に従って内部応力として扱い実験結果を説明しました。
2014年の上記実証論文では新規性は緩和体積を第一原理計算したこととされていますが、上に引用したようにすでに1999年などに行われています。